If you haven’t read the part 1 about recommender system basics, please read it here.
Collaborative filtering
The essence of collaborative filtering technique is that given enough implicit user feedback e.g click patterns, we can decipher what the user likes. Using this we can build a neighborhood and suggest what else he might like based on his past viewed items and items visited by his neighbors.
There are two types of collaborative filtering technique:
- User based
- Item based
For generating recommendations using collaborative filtering, first, you would create a similarity matrix. In the case of item based collaborative filtering, you would create a matrix that will tell the similarity between two items, based on how the users have visited two items. Similarly, in user based collaborative filtering, you would create a matrix that will tell the similarity between two users, based on the items these users visited.
There is not much difference when creating the similarity matrix for these techniques. The way you use them for recommendation is slightly different.
Co-occurence matrix based collaborative filtering
Jaccard Index
The simplest way to explain Jaccard index is that if you have two sets of users - users_i & users_j
jaccard_index = users_i.intersection(user_j) / users_i.union(users_j)Matrix factorization
The crux of matrix factorization is that you can split a huge sparse implicit data matrix into two smaller matrices.
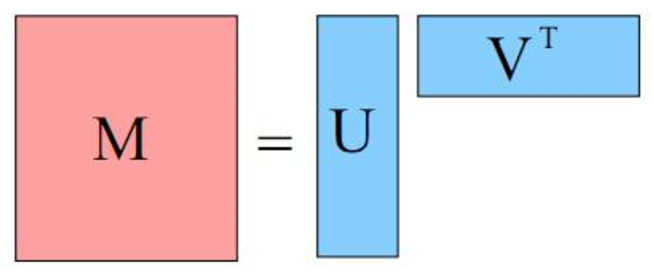
Now each of these two smaller matrix U & VT represents user’s factor and item’s factor. When making a recommendation from this matrix, you can 1xk user matrix row with kx1 items matrix row, to get the score for any user-item pair.
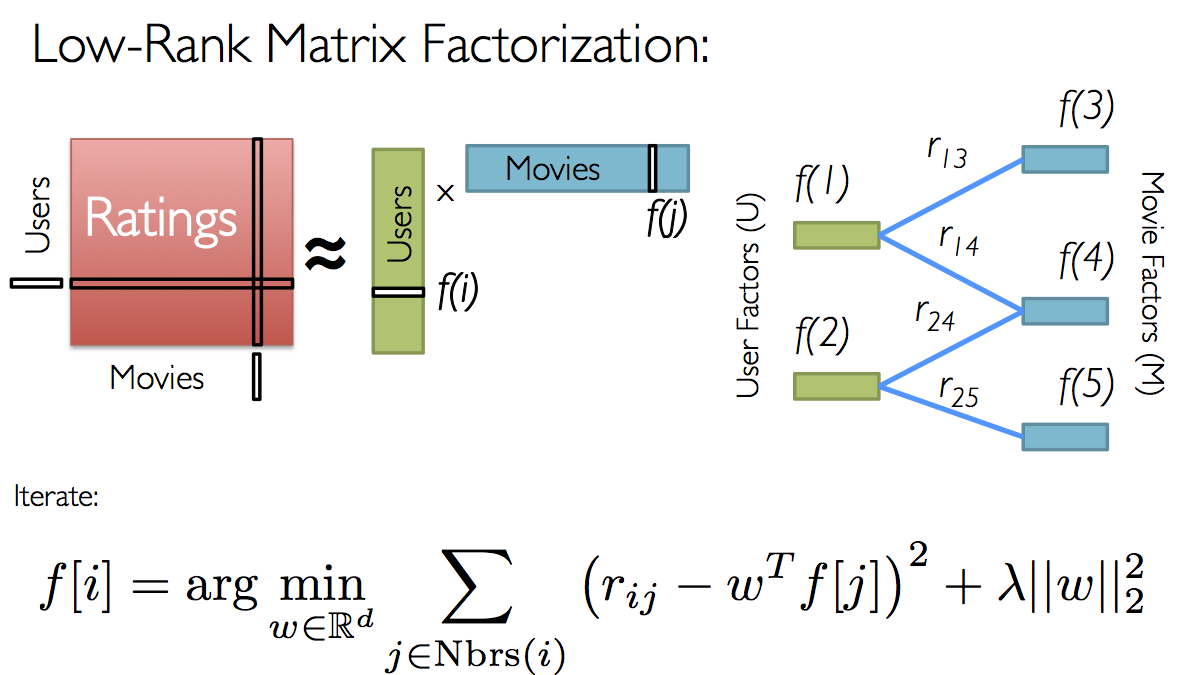
Scaling Matrix factorization
Alternating Least Squares (ALS)
In an SGD (Stochastic Gradient descent) approach, for each example in the dataset, you compute the error and then you update the parameters by a factor in the opposite direction of the gradient.
Alternating Least Squares (ALS) represents a different approach to optimizing the loss function. The key insight is that you can turn the non-convex optimization problem into an “easy” quadratic problem. ALS fixes each one of those alternatively. When one is fixed, the other one is computed, and vice versa.
Mahout ALS
You can find Mahout ALS implementation here. Running als in mahout is as simple as:
mahout parallelALS --input $als_input --output $als_output --lambda 0.1 --implicitFeedback true --alpha 0.8 --numFeatures 2 --numIterations 5 --numThreadsPerSolver 1 --tempDir tmp
Spark MLLib als
You can find Spark mllib ALS implementation here.
from pyspark.mllib.recommendation import ALS, MatrixFactorizationModel, RatingYou can also find a tutorial notebook here.
Python ALS
You can find python ALS implementation here.
import implicit
# initialize a model
model = implicit.als.AlternatingLeastSquares(factors=50)
# train the model on a sparse matrix of item/user/confidence weights
model.fit(item_user_data)
# recommend items for a user
recommendations = model.recommend(userid, item_user_data.T)
# find related items
related = model.similar_items(itemid)